(챕터 1은 파이썬의 기초와 문법, numpy와 matplotlib모듈에 대한 내용이며, 이 부분은 다루지 않겠다.)
(퍼셉트론이란?)
퍼셉트론이란, 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 구조를 말하며 '단순 퍼셉트론', '인공 뉴런' 등으로 불린다.

위의 사진과 같이 퍼셉트론을 하나의 수식으로 나타낼 수 있으며 x1, x2는 입력 신호, w1, w2는 가중치, y는 출력 신호, 세타(theta)는 임계값을 나타낸다.
수식을 보면 알 수 있듯이 입력값과 그에 맞는 가중치의 곱의 합이 임계값을 넘어서면 1을 출력값을 가지고, 넘지 못하면 0을 가지는 단순한 구조이다.
여기서 각 입력값들은 고유의 가중치들을 가지며(x1 w1, x2 w2) 가중치는 각 입력값들이 결과에 미치는 영향을 조절하는 역할을 한다. 즉, 가중치가 클수록 그 입력값의 결과에 미치는 영향이 커지는 것이다.
(단순한 논리 회로)
1. AND Gate
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. NAND Gate
| x1 | x2 | y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
3. OR Gate
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(퍼셉트론 구현하기)
먼저, AND 게이트를 구현하려면 (w1, w2, theta) = (0.5, 0.5, 0.7) 가 되면 AND 게이트가 구현된다.
실제로, 예시를 하나 들어서 (x1, x2) = (1, 0) 이라고 가정하고 앞서 수식에 대입해보면, 1 * 0.5 + 0 * 0.5 = 0.5 이므로 0.7 보다 작으므로 출력값이 0이 된다.
이렇게 가중치를 적절하게 조정만 하면, 입력값을 넣으면 그에 맞는 원하는 출력값을 내뱉는 구조의 퍼셉트론을 만들 수 있다는것을 알 수 있다.
이제 편향이라는 개념을 도입하도록 하겠다.

앞서 설명한 위의 퍼셉트론 식에서 theta 를 좌변으로 넘기면 좌변에 -theta 가 더해지고 우변은 0이 된다. 이 -theta를 b(편향) 이라고 하고 식을 재정리해보면

아래와 같은 형태의 퍼셉트론 식이 완성된다. 위의 식과 달라진건 아무것도 없지만, theta를 이용하여 편향이라는 새로운 개념을 만들어 낸 것이다.
이제 가중치와 편향에 대한 의미를 다시 한번 정리해보자면, 가중치는 앞서 말한것처럼 각 입력값의 영향력을 조절하고, 편향은 신호의 활성화정도(결과로 1을 출력하는지 안하는지) 를 나타낸다고 볼 수 있겠다.
이제 가중치와 편향을 이용해서 AND 게이트를 다시한번 나타내보자. (w1, w2, b) = (0.5, 0.5, -0.7) 을 만족하면 AND 게이트가 된다는것을 알 수 있다. (예시는 들지않겠다.)
나머지 게이트들도 나타내보면,
NAND 게이트는 NOT AND 게이트이며, 이름 그대로 입력값에 따른 출력값이 AND 게이트의 출력값의 반대이다. 따라서 가중치와 편향의 값도 반대로만 설정해주면 된다. 따라서, (w1, w2, b) = (-0.5, -0.5, 0.7) 을 만족하면 NAND 게이트가 된다는것을 알 수 있다.
OR 게이트는 (w1, w2, b) = (0.5, 0.5, -0.2) 를 만족하면 된다는것을 알 수 있다.
참고로, 앞서 나타낸 게이트들의 가중치와 편향의 조합은 수없이 많다. 그 많은 조합중 하나를 예시로 들어 나타낸 것 이니 본인이 직접 가중치와 편향을 조정해서 나타내보는것도 좋은 실습이 될 것 같다.
(퍼셉트론의 한계)
게이트를 조금 공부해본 사람이라면 한가지 의문이 들 것이다. 앞서 3가지 게이트(AND, NAND, OR) 를 설명했지만 사실 하나가 더 있다. 바로, XOR 게이트이다.
XOR 게이트를 위와 같이 표로 나타내보면
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
위와 같이 나타내어진다.
두 개의 입력값중, 어느 하나라도 1이면 1을 출력값으로 가진다는것을 알 수 있는데, 3가지 게이트들을 퍼셉트론의 가중치와 편향을 조정해서 나타낸 것 처럼 XOR 게이트도 나타내보고 싶지만, 아쉽게도 불가능하다.
이 책에서는 그 이유를 그래프를 그려서 설명하고 있다.
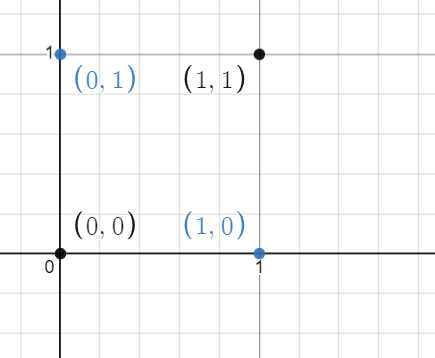
위의 사진은 (0, 0), (0, 1), (1, 0), (1, 1) 점들을 그래프상에 나타낸 것 이다.
1을 출력하는 점은 파란색으로, 0을 출력하는 점은 검은색으로 나타내었고, XOR 게이트를 의미한다는것을 알 수 있다.
이제, 여기서 퍼셉트론의 식을 다시한번 되돌아보자. 식의 형태만 가져온다면, w1 * x1 + x2 * w2 + b 의 형태인것을 우리는 알고있다.
따라서 이 퍼셉트론 형태를 함수로 생각해본다면 가중치는 기울기, 편향은 y절편과 같은 역할을 하며, 일차함수(직선) 으로 나타내어진다는것을 알 수 있다. (실제로 가중치가 기울기, 편향이 y절편의 역할을 정확히 하는것은 아니지만, 이해를 돕기위해 그렇게 생각해도 무방하다.)
그러나 위의 그래프에서 파란색 점(1) 과 검은색 점(0) 은 한 직선으로 나뉠 수 없고, 따라서 일반적인 단순 퍼셉트론의 가중치와 편향값을 조절한다고해서 XOR 게이트를 나타낼 수 없는 것이다.
말이 어렵고, 필자의 설명이 난해하여 이해가 힘들 수 있다. 이런 자세한 이유까지는 꼭 알 필요가 없으니 XOR 게이트는 나머지 게이트들과 달리, 한개의 단순 퍼셉트론으로는 나타낼 수 없다는 사실만 기억하면 된다.
(다층 퍼셉트론)
하나의 퍼셉트론으로 XOR 게이트를 표현할 수 없었지만, 여러개의 퍼셉트론으로 XOR 게이트를 구현해보는 아이디어를 제시해볼 수 있다. 그리고, 그 아이디어를 실현해 볼 계획이다.
퍼셉트론을 여러 개 쌓아 나타낸 구조를 다층 퍼셉트론 이라고 한다. 퍼셉트론을 쌓음으로서 복잡성이 늘어나고, 그에 따라 여러 가지 다양한 흐름들을 구현할 수 있다.
일단, XOR 게이트를 구현하는 방법은 다양하지만 그중 XOR 게이트를 제외한 나머지 3개의 게이트(AND, NAND, OR) 의 퍼셉트론을 쌓아올려 구현하는 방법이 있다.
| x1 | x2 | s1 | s2 | y |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
위의 표를 보면 x1, x2의 값에 따른 y값이 XOR 게이트를 만족한다는 것을 알 수 있다.
여기서 s1은 NAND 게이트에 x1, x2값을 넣어 나온 출력값이고, s2는 OR 게이트에 x1, x2값을 넣어 나온 출력값이다. 그리고 s1, s2를 AND 게이트에 넣어 나온 값이 최종 y이이다.
이렇게 한 단계가 아닌 여러 단계를 거쳐 최종적으로 XOR 게이트를 구현할 수 있게 되었다.
이렇게 한 개의 퍼셉트론이 아닌 여러개의 퍼셉트론을 쌓아, 다층의 퍼셉트론으로 XOR 게이트를 구현해보았다.
'인공지능 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| (Chapter 6) 학습 관련 기술들 (0) | 2022.08.22 |
|---|---|
| (Chapter 5) 오차역전파법 (0) | 2022.08.14 |
| (Chapter 4) 신경망 학습 (0) | 2022.08.06 |
| (Chapter 3) 신경망 (0) | 2022.08.02 |
| 책 읽기 시작 (0) | 2022.07.31 |